Question

Vectors u = −2(cos 30°i + sin30°j), v = 6(cos 225°i + sin225°j), and w = 8(cos 120°i + sin120°j) are given. Use exact values when evaluating sine and cosine.Part A: Find −7u • v. Show your work. (4 points)Part B: Use the dot product to determine if u and w are parallel, orthogonal, or neither. Justify your answer. (6 points)

Answer 1

Step-by-step explanation

let

`\begin{gathered} u=-2\mleft(\cos 30\degree i+\sin 30\degree j\mright) \\ v=6\mleft(\cos 225\degree i+\sin 225\degree j\mright) \\ w=8\mleft(\cos 120\degree i+\sin 120\degree j\mright) \end{gathered}`

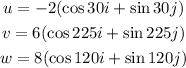
Step 1

Part A)Find −7u • v.

the dot product is the sum of the products of the corresponding entries of the two sequences of numbers,and to multiply a vector by a scalar, multiply each component by the scalar.

`(ai+bj)\cdot(ci+dj)=ac+bd`

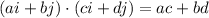
so

`\begin{gathered} -7u\cdot v \\ \text{hence} \\ -7u=-7(-2\mleft(\cos 30\degree i+\sin 30\degree j\mright))=14(\cos 30\degree i+\sin 30\degree j)=12.12i+7j \end{gathered}`

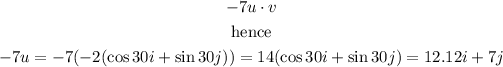
therefore, replacing

`\begin{gathered} -7u\cdot v \\ (12.12i+7j)\cdot6\mleft(\cos 225\degree i+\sin 225\degree j\mright) \\ (12.12i+7j)\cdot(-4.24i-4.24j) \\ (12.12i+7j)\cdot(-4.24i-4.24j)=(12.12\cdot-4.24)+(7\cdot-4.24)= \\ (12.12i+7j)\cdot(-4.24i-4.24j)=-51.43-29.690=-81.12 \end{gathered}`

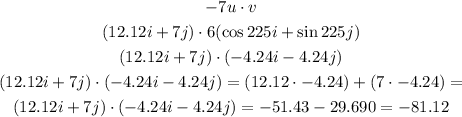
So,Part A

`-7u\cdot v=-81.12`

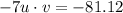
Step 2

Part B ,Use the dot product to determine if u and w are parallel, orthogonal, or neither

the dot product is also given by:

`\begin{gathered} a\cdot b=\lvert a\rvert\lvert b\rvert\cos \theta \\ so \\ \cos \theta=(a\cdot b)/(\lvert a\rvert\lvert b\rvert) \end{gathered}`

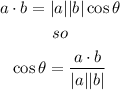
a) find the magnitude of the vectors

`\begin{gathered} \text{ }u=-2\mleft(\cos 30\degree i+\sin 30\degree j\mright), \\ u=(-2\cos 30\degree i-2\sin 30\degree j) \\ \text{hence} \\ \lvert u\rvert=\sqrt[]{(-2\cos30)^2+(-2\sin30\degree)}^2 \\ \lvert u\rvert=\sqrt[]{3^{}+1\text{ }} \\ \lvert u\rvert=\sqrt[]{4}=2 \\ \lvert u\rvert=2 \end{gathered}`

and

`\begin{gathered} \text{ w}=8\mleft(\cos 120\degree i+\sin 120\degree j\mright) \\ w=8(\cos 120\degree i+\sin 120\degree j)=-4i+6.92j \\ \text{hence} \\ \lvert w\rvert=\sqrt[]{(-4)^2+(6.92)^2} \\ \lvert w\rvert=\sqrt[]{16^{}+48} \\ \lvert w\rvert=\sqrt[]{64} \\ \lvert w\rvert=8 \end{gathered}`

c) dot product

`\begin{gathered} u\cdot w=-2(\cos 30\degree i+\sin 30\degree j)\cdot8(\cos 120\degree i+\sin 120\degree j) \\ u\cdot w=-5.73+5.92 \\ u\cdot w=0.19 \end{gathered}`

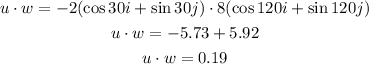
finally, replace in the formula and find the angle

`\begin{gathered} \cos \theta=(a\cdot b)/(\lvert a\rvert\lvert b\rvert) \\ \cos \theta=(0.19)/(2\cdot8) \\ \cos \theta=0.011875 \\ \theta=\cos ^(-1)(0.011875) \\ \theta=90 \end{gathered}`

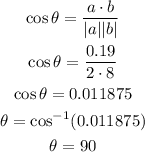
so

the vectors are orthogonal ( make a 90° angle)

I hope this helps you