Question

Consider the function f(x) = x^2 - 6x + 5

a. What are the x-intercepts of the function?

b. Does the function have a line of symmetry? if so, what is it?

c. Does the function have a maximum or minimum value? Explain how you know without graphing.​

Answer 1

Explanation:

a. the question can be factored as (x-5)(x-1) so the 2 x intercepts are 5 and 1

b. yes the function has a line of symmetry every parabola does and it is at when x is 3

x. the function has a minimum value because the equation has x^2 which is 1x^2 1 is a positive meaning that the function opens upward which means it has a minimum value

Answer 2

A)

(1, 0) and (5, 0)

B)

Yes.

The equation is x = 3.

C)

Yes.

In this case, we have a minimum.

Explanation:

We are given the function:

`f(x)=x^2-6x+5`

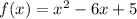
Since the highest degree is two, we can immediately determine this to be a quadratic.

A)

The x-intercepts of a function are whenever the function equates to 0. Hence:

`0=x^2-6x+5`

We can factor:

`(x-1)(x-5)=0`

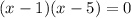
Zero Product Property:

`x-1=0\text{ or } x-5=0`

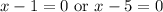
Solving yields:

`x=1 \text{ and } x=5`

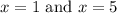
So, our x-intercepts are at (1, 0) and (5, 0).

B)

Since this is a quadratic, it indeed has a line of symmetry.

Recall that the line of symmetry for a quadratic equivalent to the x-coordinate of the vertex.

In the given function, a = 1, b = -6, and c= 5.

Hence, the x-coordinate of the vertex is:

`\displaystyle x=-(b)/(2a)=-((-6))/(2(1))=(6)/(2)=3`

So, the line of symmetry is x = 3.

C)

Every parabola has a minimum/maximum value.

This depends on the sign of the leading coefficient.

If the leading coefficient is positive, then we have a minimum since our parabola will be curving upwards.

And if the leading coefficient is negative, then we have a maximum since our parabola will be curving downwards.

Since our leading coefficient here is 1, hence positive, we have a minimum value.