Answer:
The roots are x = -4, 1 and 3.
B is the correct option.
Explanation:
We have to find the roots of the polynomial
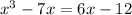
We can find the roots by forming a system of equations and with the help of a graphing calculator.
The system of equations for the given polynomial:
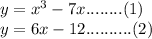
Now, we graph these equations in the xy-plane. The x-coordinate (s) of the intersection point will be the roots of the equation.
The graph is shown in the attached file.
The intersection points are (-4,-36),(1,-6) and (3,6). The x-coordinates are x = -4,1 and 3.
Therefore, the roots are x = -4, 1 and 3.
B is the correct option.