Question

Why would a MacLauren series for f(x) = x^2*e^x^2 be 0 at f^(7)(0) and f^(9)(0) but 8!/3! at f^(8)(0)? I know how to find the series (x^2e^2^2 = x^2 + x^4 + x^6/2! + x^8/3! + ... you basically take the MacLauren series for e^x, modify it for e^x^2, and then multiply that by x^2). I'm just confused why it's 8!/3! at f^(8)(0). Shouldn't it be 0 as well since f^(8)(0) = x^18/8! and if x = 0 then 0^18/8! = 0? What am I missing?

Answer 1

By definition, the Maclaurin series for
`f(x)` is


`\displaystyle\sum_(n=0)^\infty(f^((n))(0)x^n)/(n!)`

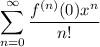
It sounds to me like you're asking why
`f^((n))(0)` is zero for some terms, and non-zero for others. Take the derivative to see why this is the case.


`f(x)=f^((0))(x)=x^2e^(x^2)`

`f^((1))(x)=2xe^(x^2)+x^2(2x)e^(x^2)=(2x+2x^3)e^(x^2)`

`f^((2))(x)=(2+6x^2)e^(x^2)+(2x+2x^3)(2x)e^(x^2)=(2+10x^2+4x^4)e^(x^2)`

`f^((3))(x)=(20x+16x^3)e^(x^2)+(2+10x^2+4x^4)(2x)e^(x^2)=(24x+36x^3+8x^4)e^(x^2)`

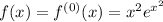
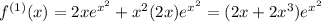
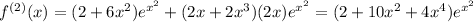
and so on. There's a pattern here. Every odd-order derivative involves an odd-degree polynomial multiplied by
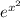
`e^(x^2)` with no constant term. So
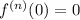
`f^((n))(0)=0` when
`n` is odd. Meanwhile, every even-order derivative consists of an even-degree polynomial multiplied by
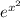
`e^(x^2)` and *does* have a constant term, which is why
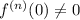
`f^((n))(0)\\eq0` when
`n` is even.

This would explain the absence of odd powers of
`x` in the series expansion for
`f(x)`.

But you can see why this must happen just by referring to the manipulated series for
`e^x`:


`e^x=\displaystyle\sum_(n=0)^\infty(x^n)/(n!)=x^0+x^1+\frac{x^2}2+\frac{x^3}6+\cdots`
(both even and odd powers)


`e^(x^2)=\displaystyle\sum_(n=0)^\infty(x^(2n))/(n!)=x^0+x^2+\frac{x^4}2+\frac{x^6}6+\cdots`
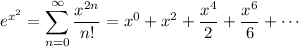
(even powers only)


`x^2e^(x^2)=\displaystyle\sum_(n=0)^\infty(x^(2(n+1)))/(n!)=x^2+x^4+\frac{x^6}2+\frac{x^8}6+\cdots`
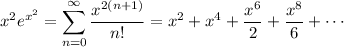
(again, even powers only)

So when
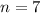
`n=7` or
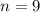
`n=9`, the corresponding term in the series is 0, but this is not the case for when
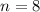
`n=8` or any other even number.