Question

What is the equation of a line perpendicular to 5y= -3x-10 passing through the point (3,-6)

Answer 1

In this case the answer is very simple .

Step 01:

Data

equation of the given line: 5y = -3x -10

y = -3/5x - 2

m = -3/5

given point: (3,-6) x1 = 3 y1 = -6

Step 02:

Slope of the perpendicular line, m’

m' = (-1) / m

`m\text{'}=(-1)/(-(3)/(5))=(5)/(3)`

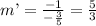
Point-slope form of the line

(y - y1) = m (x - X1)

`(y\text{ - (-6)) = }(5)/(3)\cdot(x-3)\text{ }`
`\begin{gathered} y\text{ +6=}(5)/(3)x\text{ -}(5)/(3) \\ y\text{ = }(5)/(3)x\text{ -}(5)/(3)-6 \\ \end{gathered}`
`y\text{ = }(5)/(3)x\text{ -}(23)/(3)`

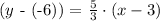
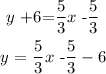
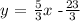
The answer is:

The equation of the perpendicular line is:

y = (5/3) x - (23/3)