In this case the answer is very simple .
Step 01:
Data
equation of the given line: 5y = -3x -10
y = -3/5x - 2
m = -3/5
given point: (3,-6) x1 = 3 y1 = -6
Step 02:
Slope of the perpendicular line, m’
m' = (-1) / m
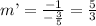
Point-slope form of the line
(y - y1) = m (x - X1)
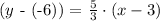
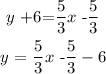
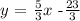
The answer is:
The equation of the perpendicular line is:
y = (5/3) x - (23/3)