Question

How many, and what type of, solutions does 3x2−x−5=0 have?

1 rational solution

2 irrational solutions

2 rational solutions

2 nonreal solutions

Answer 1

B: 2 irrational solutions

Answer 2

The correct option is 2 and the solutions of given equation are irrational.

Explanation:

The given equation is

`3x^2-x-5=0`

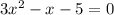
If an equation is defined as

`ax^2+bx+c=0`

Then the quadratic formula is

`x=(-b\pm √(b^2-4ac))/(2a)`

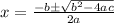
The value of discriminant for the given equation is

`x=(-(-1)\pm √((-1)^2-4(3)(-5)))/(2(3))`

`x=(1\pm √(61))/(6)`

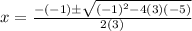
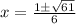
Since
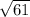`√(61)` is an irrational number, therefore the addition and division with an irrational number is irrational.

So, both the solutions of given equation are irrational and option 2 is correct.