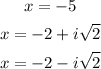Question

Find all zeros of the polynomial P(x) = x3 + 9x2 + 26x + 30x =

Answer 1

Given: A polynomial

`P(x)=x^3+9x^2+26x+30`

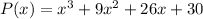
Required: To determine the zeroes of the polynomial.

Step-by-step explanation: To solve a cubic equation, we need to determine three zeroes of the equation.

We will use the hit and trial method to determine the first zero(s).

From the factors of 30, we have the following factors, which can be a zero of the equation-

`\pm1,\pm2,\pm3,\pm5\pm10,\pm15,\pm30`

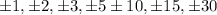
We can see that for x=-5, P(x)=0, indicating that our first zero is x=-5.

Since x=-5 is a zero of the polynomial, then x+5 is a factor of the polynomial (By factor theorem).

Hence we can divide the polynomial by x+5 to reduce it to a quadratic equation as follows-

Hence, the polynomial is reduced to-

`P(x)=(x+5)(x^2+4x+6)`

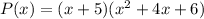
Now to find the zeroes, we put P(x)=0,

`\begin{gathered} (x+5)(x^2+4x+6)=0 \\ x+5=0\Rightarrow x=-5\text{ or} \\ x^2+4x+6=0 \end{gathered}`

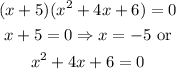
We will use the quadratic formula to find the roots of the quadratic equation-

`\begin{gathered} x=(-4\pm√(16-24))/(2) \\ =(-4\pm2i√(2))/(2) \\ =-2\pm i√(2) \end{gathered}`

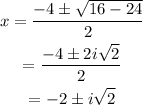
Final Answer: Zeroes of the polynomial are

`\begin{gathered} x=-5 \\ x=-2+i√(2) \\ x=-2-i√(2) \end{gathered}`