Question

17. A cash box had an equal number of dimes and quarters. It had twice as many penniesand three times as many nickels, The total cash was $416. How many nickels werethere?Answer

Answer 1

We have to find how many nickels were in the box.

Lets call D to the number od dimes, Q to the number of quarters, P to the number of pennies and N to the number of nickels.

We know that it has equal number of dimes and quarters. Then, we can write:

`D=Q`

We also know that it has twice as many pennies and three times as many nickels. We assume that is referring to as many as dimes, so we can write two equations from this:

`\begin{gathered} P=2\cdot D \\ N=3\cdot D \end{gathered}`

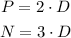
We then know that the total sum of cash is equal to $416. As each coin has a value, we can multiply the number if coins by its corresponding value and add them, and this should be equal to the cash amount.

The value of each coin is:

- A penny (P) is worth 1 cent.

- A nickel (N) is worth 5 cents.

- A dime (D) is worth 10 cents.

- A quarter (Q) is worth 25 cents.

Then, we can write:

`0.01\cdot P+0.05\cdot N+0.10\cdot D+0.25\cdot Q=416`

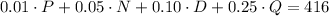
We want to find the value of N, the number of nickels. We know that is 3 times the number of dimes.

Then, we can write the number of each coin in function of the number of dimes as:

`\begin{gathered} N=3\cdot D\Rightarrow D=(1)/(3)N \\ Q=D=(1)/(3)N \\ P=2\cdot D=(2)/(3)N \end{gathered}`

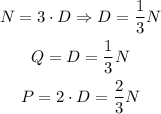
Then, replacing in the last equation, we get an equation with N as unknown:

`\begin{gathered} 0.01\cdot P+0.05\cdot N+0.10\cdot D+0.25\cdot Q=416 \\ 0.01\cdot((2)/(3)N)+0.05\cdot N+0.10\cdot((1)/(3)N)+0.25\cdot((1)/(3)N)=416 \\ 0.01\cdot2N+3\cdot0.05N+0.10N+0.25N=3\cdot416 \\ (0.02+0.15+0.10+0.25)\cdot N=1248 \\ 0.52\cdot N=1248 \\ N=(1248)/(0.52) \\ N=2400 \end{gathered}`

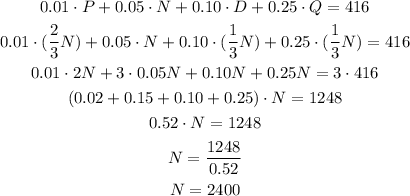
Answer: there were 2400 nickels in the cash box.