You're looking for
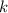
such that
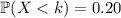
Transforming the standard normal distribution, you have
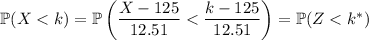
where
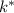
is the cutoff score in terms of this new distribution. The z-score corresponding to a probability of 0.20 is approximately
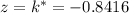
, which means the cutoff test score is
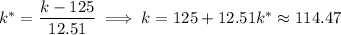
Rounding to the nearest whole point, a score of about 114 is the bare minimum requirement to not have to take the remedial course.