Question

The population of a species of starfish in the Gulf of Mexico is decreasing at an exponential rate, A(t) = A0e(kt) . Five years ago the population was 10,000, in 2015 it is only 2000. When the population is 500, the starfish population cannot recover. When will this event occur?

Show your work and explain the process of solving this problem.

Answer 1

Answer: 4.3 years

Explanation:

Given: The population of a species of starfish in the Gulf of Mexico is decreasing at an exponential rate

To find the population we have given an equation
`A(t) = A_0e{kt}`, where k is the decay rate (k<0) in t years and
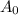`A_0` is the initial population.

Five years ago the population was 10,000, in 2015 it is only 2000.

So put t=5 ,
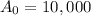`A_0=10,000` and A(t)= 2000 in the above function we get

`2000=10,000e^(5k)\\\\\Rightarrow e^(5k)=0.2`

Taking log on both sides, we get

`5k=\log(0.2)\\\\\Rightarrow5k=-0.698970004336\\\\\Rightarrow\ k=-0.139794000867`

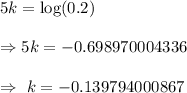
Taking 2015 as the initial year
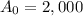`A_0=2,000`, To find t when A(t)=500

`500=2000e^(-0.139794000867t)\\\\\Rightarrow e^(-0.139794000867t)=0.25`

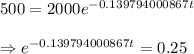
Taking log on both sides, we get

`-0.139794000867t=\log(0.25)\\\\\Rightarrow-0.139794000867t=-0.602059991328\\\\\Rightarrow t=(-0.602059991328)/(-0.139794000867)\\\\\Rightarrow t=4.30676558074\approx4.3\ years`

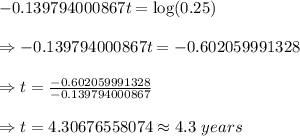
Hence, This event will occur in 4.3 years from 2015.

Answer 2

first is to solve the value of k
when A0 = 10000
a(t) = 2000
t = 5
using the formula
a(t) = A0 e^(kt)
2000 = 10000 e^(5k)
2000 / 10000 = e^(5k)
ln ( 1/5) = 5k
k = (ln(1/5)) / 5
k = -1.6094 /5
k = -0.3219

now solve for t,
500 = 10000 e^(-0.3219t)
ln( 500/10000) = -0.3219t
t = 9.3067 years
since that is calculated as the basis at 5 years ago
then actual t is 4.3067 years