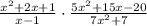Given the expression:
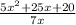
Let's determine where each piece belongs to create a rational expression equivalent to the expression given.
To determine, where each piece belong, let's input each value and simplify.
First simplify the given expression
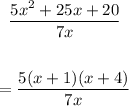
Thus, we have:
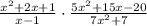
Let's simplify the expression above to verify if it is equivalent to the simplified expression of the given expression.
We have:
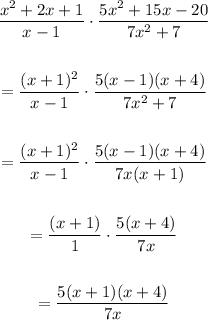
The expressions are equivalent.
Therefore, the correct expression is:
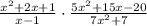
The expression in the numerator = 5x² + 15x - 20
The expression in the denominator = x - 1
ANSWER: