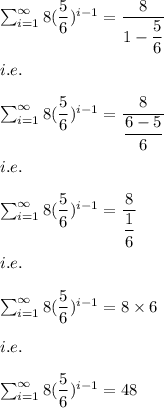Question

Identify whether the series summation of 8 open parentheses 5 over 6 close parentheses to the i minus 1 power from 1 to infinity is a convergent or divergent geometric series and find the sum, if possible. (2 points)

Answer 1

`\displaystyle\sum_(i=1)^\infty\8\left(\frac56\right)^(i-1)`

This is a geometric series with a common ratio between successive terms that is less than 1 in absolute value. This means the series will converge. The value of the sum is
`\frac8{1-\frac56}=48`.

Answer 2

Yes, the series is convergent.

The sum is: 48

Explanation:

The series is given by:

`\sum_(i=1)^(\infty) 8((5)/(6))^(i-1)`

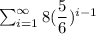
Now, each term of the series is a constant multiple of the preceding element of the series.

The constant multiple is: 5/6<1

( Since,

`a_1=8((5)/(6))^(1-1)\\\\i.e.\\\\a_1=8((5)/(6))^0\\\\i.e.\\\\a_1=8`

`a_2=8((5)/(6))^(2-1)\\\\i.e.\\\\a_2=8((5)/(6))\\\\i.e.\\\\a_2=(5)/(6)a_1`

Similarly, for nth term we have:

`a_n=(5)/(6)a_(n-1)`

)

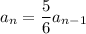
Hence, the series is a geometric series.

Also, this series is convergent.

( since the constant multiple i.e. the common ratio is less than 1)

We know that the sum of the infinite geometric series of the type:

`\sum_(n=1)^(\infty)ar^(n-1)=(a)/(1-r)`

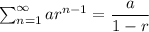
where a is the first term of the series and r is the common ratio.

Here we have:

`a=8\ and\ r=(5)/(6)`

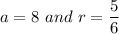
Hence, we have:

`\sum_(i=1)^(\infty) 8((5)/(6))^(i-1)=(8)/(1-(5)/(6))\\\\i.e.\\\\\sum_(i=1)^(\infty) 8((5)/(6))^(i-1)=(8)/((6-5)/(6))\\\\i.e.\\\\\sum_(i=1)^(\infty) 8((5)/(6))^(i-1)=(8)/((1)/(6))\\\\i.e.\\\\\sum_(i=1)^(\infty) 8((5)/(6))^(i-1)=8* 6\\\\i.e.\\\\\sum_(i=1)^(\infty) 8((5)/(6))^(i-1)=48`