Question

Line segment AB has endpoints A(2, 9) and B(5, 8) . A dilation, centered at the origin, is applied to AB¯¯¯¯¯ . The image has endpoints A′(43, 6) and B′(103, 163) . What is the scale factor of this dilation?

32
23
2
3

Answer 1

the answer is 2/3
i took the test
hope this helps!

Answer 2

Answer: The correct option is (B)
`(2)/(3).`

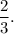
Step-by-step explanation: Given that the co-ordinates of the end-points of a line segment AB are A(2, 9) and B(5, 8). After being dilated about the origin (0, 0), the co-ordinates of the end-points of image A'B' are
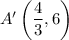`A^\prime\left((4)/(3),6\right)` and
`B^\prime\left((10)/(3),(16)/(3)\right).`

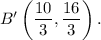
We are to find the scale factor of the dilation.

The scale factor of the dilation will be

`S=\frac{\textup{length of the image line}}{\textup{length of the original line}}.`

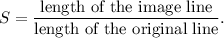
The lengths of the lines AB and A'B' are calculated using distance formula as follows:

`AB=√((5-2)^2+(8-9)^2)=√(9+1)=√(10),\\\\\\A'B'=\sqrt{\left((10)/(3)-(4)/(3)\right)^2+\left((16)/(3)-6\right)^2\right)}=\sqrt{4+(4)/(9)}=\sqrt{(40)/(9)}=(2)/(3)√(10)~\textup{units}.`

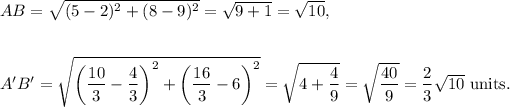
Therefore, the required scale factor of dilation is

`S=(A'B')/(AB)=((2)/(3)√(10))/(√(10))=(2)/(3).`

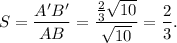
Thus, the scale factor of the dilation is
`(2)/(3).`

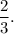
Option (B) is CORRECT.