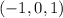Answer:
The correct answer is B.
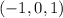
Explanation:
The given linear system is
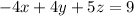
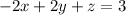
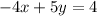
The augmented matrix is
![\left[\begin{array}{cccc}-4&4&5&|9\\-2&2&1&|3\\-4&5&0&|4\end{array}\right]](https://img.qammunity.org/2018/formulas/mathematics/college/uaemy7ri06d9hw1kn3290veokpp9raboqt.png)
To solve this by Gauss-Jordan elimination means that, we need to reduce to reduced row echelon form.
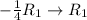
![\left[\begin{array}{cccc}1&-1&-(5)/(4) &\:\:\:\:\:\:|-(9)/(4) \\-2&2&1&|3\\-4&5&0&|4\end{array}\right]](https://img.qammunity.org/2018/formulas/mathematics/college/ad2lgqxygeyipwdvklf7nd9mm0emhoyy91.png)
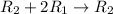
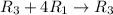
![\left[\begin{array}{cccc}1&-1&-(5)/(4) &|-(9)/(4) \\0&0&-(3)/(2) &|-(3)/(2) \\0&1&-5&|-5\end{array}\right]](https://img.qammunity.org/2018/formulas/mathematics/college/c4gplofkeewgz4rrr4xrhg2wk771imvggs.png)
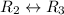
![\left[\begin{array}{cccc}1&-1&-(5)/(4) &|-(9)/(4) \\0&1&-5 &|-5 \\0&0&-(3)/(2)&|-(3)/(2)\end{array}\right]](https://img.qammunity.org/2018/formulas/mathematics/college/7toj7pd3zb08xbgkflclv9tp262edqby7a.png)
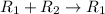
![\left[\begin{array}{cccc}1&0&-(25)/(4) &|-(29)/(4) \\0&1&-5 &|-5 \\0&0&-(3)/(2)&|-(3)/(2)\end{array}\right]](https://img.qammunity.org/2018/formulas/mathematics/college/e3hs6ph9imqdseq5qap0189chezwo2vbqc.png)
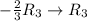
![\left[\begin{array}{cccc}1&0&-(25)/(4) &|-(29)/(4) \\0&1&-5 &|\:\:-5 \\0&0&1&|\:\:\:\:\:\:\:1\end{array}\right]](https://img.qammunity.org/2018/formulas/mathematics/college/g6pbtj9oxsnqaezf0n4bwbxf79cdb3eq13.png)
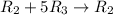
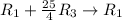
![\left[\begin{array}{cccc}1&0&0&|-1 \\0&1&0&|\:\:\:\:\:\:0\\0&0&1&|\:\:\:\:\:\:1\end{array}\right]](https://img.qammunity.org/2018/formulas/mathematics/college/2ktcyyum4hzdj5hegot5ma5db1msjsze9v.png)
The matrix is now in the reduced row echelon form.
This gives the solution to be,