Question

The normal eye, myopic eye and old age

As we age, the lens of the eye hardens and accommodation no longer occurs: it is presbyopia.
Paradoxically, with age, a nearsighted person sees better than a "normal" person.
The aim of this exercise is to explain this paradox. The eye is modeled by a constant focal
length f′0 when the eye is presbyopic and by a screen (the retina) at the distance d from the
lens (d = 15 mm).
1. A normal, presbyopic eye sees an object at infinity in focus while a myopic eye sees an
object at a distance Dm from the eye (Dm = 15 cm).
What relation do we have in the two cases between f′0 and d?
2. A presbyopic person reads a newspaper placed 25 cm from his/her eyes. The radius r0 of
the pupil of the eye is 1 mm. Calculate the diameter of the spot on the retina image from a
log point, for a myopic eye and a normal eye. Conclude​

Answer 1

1) f’₀ / f = 1.10, the relationship between the focal length (f'₀) and the distance to the retina (image) is given by the constructor's equation

2) the two diameters have the same order of magnitude and are very close to each other

Step-by-step explanation:

You have some problems in the writing of your exercise, we will try to answer.

1) The equation to be used in geometric optics is the constructor equation

`(1)/(f) = (1)/(p) + (1)/(q)`

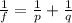
where p and q are the distance to the object and the image, respectively, f is the focal length

* For the normal eye and with presbyopia

the object is at infinity (p = inf) and the image is on the retina (q = 15 mm = 1.5 cm)

`(1)/(f'_o) = 1/ inf + (1)/(1.5)`

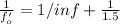
f'₀ = 1.5 cm

this is the focal length for this type of eye

* Eye with myopia

the distance to the object is p = 15 cm the distance to the image that is on the retina is q = 1.5 cm

1 / f = 1/15 + 1 / 1.5

1 / f = 0.733

f = 1.36 cm

this is the focal length for the myopic eye.

In general, the two focal lengths are related

f’₀ / f = 1.5 / 1.36

f’₀ / f = 1.10

The question of the relationship between the focal length (f'₀) and the distance to the retina (image) is given by the constructor's equation

2) For this second part we have a diffraction problem, the point diameter corresponds to the first zero of the diffraction pattern that is given by the expression for a linear slit

a sin θ= m λ

the first zero occurs for m = 1, as the angles are very small

tan θ = y / f = sin θ / cos θ

for some very small the cosine is 1

sin θ = y / f

where f is the distance of the lens (eye)

y / f = lam / a

in the case of the eye we have a circular slit, therefore the system must be solved in polar coordinates, giving a numerical factor

y / f = 1.22 λ / D

y = 1.22 λ f / D

where D is the diameter of the eye

D = 2R₀

D = 2 0.1

D = 0.2 cm

the eye has its highest sensitivity for lam = 550 10⁻⁹ m (green light), let's use this wavelength for the calculation

* normal eye

the focal length of the normal eye can be accommodated to give a focus on the immobile retian, so let's use the constructor equation

\frac{1}{f} = \frac{1}{p} + \frac{1}{q}

sustitute

`(1)/(f) = (1)/(25) + (1)/(1.5)`

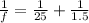
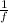`(1)/(f)`= 0.7066

f = 1.415 cm

therefore the diffraction is

y = 1.22 550 10⁻⁹ 1.415 / 0.2

y = 4.75 10⁻⁶ m

this is the radius, the diffraction diameter is

d = 2y

d_normal = 9.49 10⁻⁶ m

* myopic eye

In the statement they indicate that the distance to the object is p = 15 cm, the retina is at the same distance, it does not move, q = 1.5 cm

`(1)/(f) = (1)/(15) + (1)/( 1.5)`

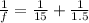
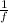`(1)/(f)`= 0.733

f = 1.36 cm

diffraction is

y = 1.22 550 10-9 1.36 10-2 / 0.2 10--2

y = 4.56 10-6 m

the diffraction diameter is

d_myope = 2y

d_myope = 9.16 10-6 m

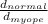`(d_(normal))/(d_(myope))` = 9.49 /9.16

\frac{d_{normal}}{d_{myope}} = 1.04

we can see that the two diameters have the same order of magnitude and are very close to each other