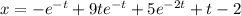Question

X"+2x'+x=5e^-2t+t, x(0)=2, x'(0)=1

Answer 1

First, find the characteristic solution. The characteristic equation for this ODE is


`r^2+2r+1=(r+1)^2=0`

which has one root at
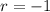
`r=-1` with multiplicity 2. This means the characteristic solution takes the form


`x_c=C_1e^(-t)+C_2te^(-t)`

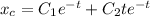
There's no conflict with the nonhomogeneous part, which means you can guess a particular solution with undetermined coefficients of the form


`y_p=ae^(-2t)+bt+c`

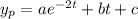
which has derivatives


`{y_p}'=-2ae^(-2t)+b`

`{y_p}''=4ae^(-2t)`

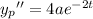
Substituting the particular solution into the ODE yields


`4ae^(-2t)+2(-2ae^(-2t)+b)+ae^(-2t)+bt+c=5e^(-2t)+t`

`ae^(-2t)+bt+2b+c=5e^(-2t)+t`

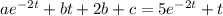
Matching up coefficients gives a system of equations with solution


`\begin{cases}a=5\\b=1\\2b+c=0\end{cases}\implies a=5,b=1,c=-2`

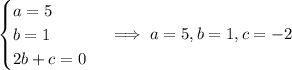
so that the particular solution is


`x_p=5e^(-2t)+t-2`

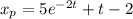
which in turn means the general solution is


`x=x_c+x_p`

`x=C_1e^(-t)+C_2te^(-t)+5e^(-2t)+t-2`

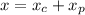
Use the initial conditions to solve for the remaining constants.


`\begin{cases}2=C_1+3&x(0)=2\\1=-C_1+C_2-9&x'(0)=1\end{cases}\implies C_1=-1,C_2=9`

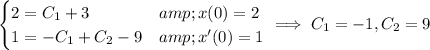
Therefore the solution to this IVP is


`x=-e^(-t)+9te^(-t)+5e^(-2t)+t-2`