Question

If a sphere of ice cream that was 2.5 inches in diameter was placed on top of the ice cream cone that had a height of 4 inches and a diameter of 1.75 inches and left to melt directly into the cone, would the all of the ice cream fit into the cone? Justify your answer using mathematics and a complete sentence answer.

Answer 1

The cone would not the all of the ice cream fit into the cone.

Explanation:

Geometrically speaking, the volume of the cone (
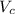`V_(c)`), measured in cubic inches, is described by the following equation:

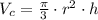`V_(c) = (\pi)/(3)\cdot r^(2)\cdot h` (1)

Where:

`r` - Base radius, measured in inches.

`h` - Height, measured in inches.

And the ice cream ball is described by the volume equation for the sphere (
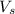`V_(s)`), measured in cubic inches:

`V_(s) = (4\pi)/(3) \cdot R^(3)` (2)

Where
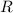`R` is the radius of the ice cream ball, measured in inches.

In this case, the ice cream will fit into the cone if and only if
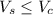`V_(s) \le V_(c)`. That is:

`(4\pi)/(3)\cdot R^(3) \le (\pi)/(3)\cdot r^(2)\cdot h`

`4\cdot R^(3) \le r^(2)\cdot h`

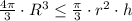
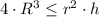
If we know that
`r = 0.875\,in`,
`h = 4\,in` and
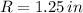`R = 1.25\,in`, then the inequation is:

`4\cdot (1.25\,in)^(3)\le (0.875\,in)^(2)\cdot (4\,in)`

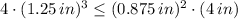
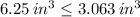`6.25\,in^(3)\le 3.063\,in^(3)` (CRASH!)

Which leads to an absurd. Hence, the cone would not the all of the ice cream fit into the cone.