Answer : The number of nickel and dimes in the jar are, 12 and 8 respectively.
Step-by-step explanation :
As we are given that:
Number of nickels = n
Number of dimes = d
As, there are 20 coins in the jar. The equation will be:
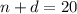 .........(1)
.........(1)
or,
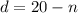 ............(2)
............(2)
Total value of the coins is $1.40. The equation will be:
As we know that:
1 dime = $ 0.1
1 nickel = $ 0.05
So,
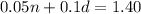 ........(3)
........(3)
Now put equation 2 in equation 3, we get:
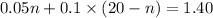
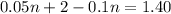
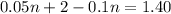
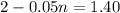

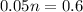
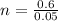

Now put the value of 'n' in equation 2, we get:
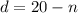

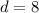
Thus, the number of nickel and dimes in the jar are, 12 and 8 respectively.