The formula for the margin of error is
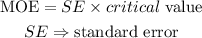
The critical value for 95% confidence interval is 1.96
The standard error is
![\begin{gathered} SE=\frac{\sigma}{\sqrt[]{n}} \\ \sigma\Rightarrow standard\text{ deviation} \\ n\Rightarrow\text{sample size} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/yshdvhh75aihq19ervew.png)
To know which of the list of options will yield approximately the desired margin of error, we will have to calculate the margin of error with the following values
For 110 trees, n= 110, standard dev. =16
![\begin{gathered} SE=\frac{16}{\sqrt[]{110}}=1.53 \\ \text{MOE}=1.53*1.96=2.9988 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/usei59rw1oga0zc15jqr.png)
For 144 trees, n=144, standard dev=16
![\begin{gathered} SE=\frac{16}{\sqrt[]{144}}=(16)/(12)=1.33 \\ \text{MOE}=1.33*1.96=2.61 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/tll5vkkfrmcewr8bmxtq.png)
For 43 trees, n=43 , standard dev.=16
![\begin{gathered} SE=\frac{16}{\sqrt[]{43}}=2.44 \\ \text{MOE}=2.44*1.96=4.782 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/1ef91w9rzlexgtb80zml.png)
For 87 trees, n= 87, standard dev=16
![\begin{gathered} SE=\frac{16}{\sqrt[]{87}}=1.72 \\ \text{MOE}=1.72*1.96=3.3712 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/fcebnci32ut8kc3fe1eb.png)
Hence, from the above calculations, the most prefered is the sample size of 110 trees (because the margin of error of 2.9988 is approximately 3 )
Answer is 110 trees