Question

Suppose the coefficient of kinetic friction between mA and the plane in the figure(Figure 1) is μk = 0.15, and that mA=mB=2.7kg. part aAs mB moves down, determine the magnitude of the acceleration of mA and mB, given θ = 30 ∘ .part b What smallest value of μk will keep the system from accelerating?

Answer 1

We are asked to determine the acceleration of the system. To do that we will consider the two masses to be a single system and we will use the following free-body diagram.

Where:

`\begin{gathered} W_b=\text{ weight of B} \\ W_a=\text{ weight of A} \\ W_(ah)=\text{ component of the weight of A in the horizontal direction} \\ W_(av)=\text{ component of the weight of B in the vertical direction} \\ N=\text{ normal force} \\ F_f=\text{ force of friction} \end{gathered}`

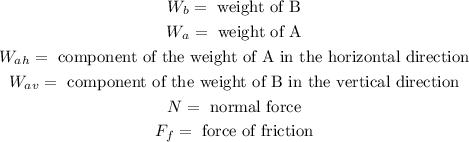
To determine the components of the weight of "A" we use the following triangle:

Therefore, the vertical component is given by:

`W_(av)=W_a\cos30`

Since the weight is the product of the mass and the acceleration we have;

`W_(av)=m_ag\cos30`

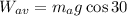
The horizontal component is given by:

`W_(ah)=W_a\sin30`

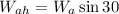
Substituting the formula for weight:

`W_(ah)=m_ag\sin30`

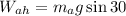
The friction force is given by:

`F_f=\mu N`

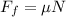
The normal force "N" is equivalent to the vertical component of the weight since there is no acceleration in that direction. Therefore, we have:

`F_f=\mu W_(av)`

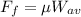
Substituting the values:

`F_f=\mu m_ag\cos30`

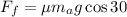
Now, the net force is equivalent to the forces acting on the system. Therefore, the net force is:

`F_(net)=m_bg-F_f-W_(ah)`

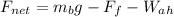
Substituting we get:

`F_(net)=m_bg-\mu m_ag\cos30-m_ag\sin30`

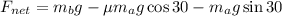
According to Newton's second law we have that the net force is equal to the product of the mass and the acceleration:

`F_(net)=ma`

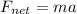
The total mass is the sum of the masses "A" and "B".

`F_(net)=(m_a+m_b)a`

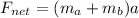
Substituting the net force:

`m_bg-\mu m_ag\cos30-m_ag\sin30=(m_a+m_b)a`

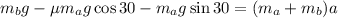
Now, we divide both sides by the total mass:

`(m_bg-\mu m_ag\cos30-m_ag\sin30)/(m_a+m_b)=a`

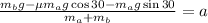
Since we have that the masses are equal:

`m_a=m_b=m`

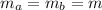
Substituting we get:

`(mg-\mu mg\cos(30)-mg\sin(30))/(m+m)=a`

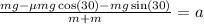
Adding the masses in the denominator:

`(mg-\mu mg\cos(30)-mg\sin(30))/(2m)=a`

We can cancel out the "m":

`(g-\mu g\cos(30)-g\sin(30))/(2)=a`

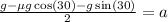
Now, we plug in the values:

`(9.8(m)/(s^2)-(0.15)(9.8(m)/(s^2))\cos30-9.8(m)/(s^2)\sin30)/(2)=a`

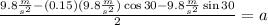
Solving the operations:

`1.81(m)/(s^2)=a`

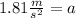
Therefore, the acceleration is 1.81 meters per second square.

Part B. To determine the value of the coefficient of friction that will keep the system from accelerating we must go back to the formula for the acceleration:

`(g-\mu g\cos(30)- g\sin(30))/(2)= a`

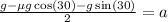
Now, we will set the acceleration to zero:

`(g-\mu g\cos(30)- g\sin(30))/(2)=0`

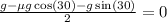
Multiplying both sides by 2:

`g-\mu g\cos(30)-g\sin(30)=0`

Now, we can divide both sides by "g":

`1-\mu\cos30-\sin30=0`

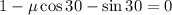
Now, we solve for the coefficient of friction. We subtract 1 to both sides:

`-\mu\cos(30)-\sin(30)=-1`

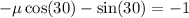
Now, we add sin(30) to both sides:

`-\mu\cos(30)=-1+\sin(30)`

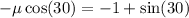
Now, we divide both sides by -cos(30):

`\mu=(-1+\sin(30))/(-\cos(30))`

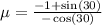
Now, we solve the operations:

`\mu=0.58`

Therefore, the friction coefficient is 0.58