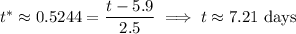The 70th percentile is the same as the cutoff recovery time
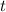
such that every point above this time falls in the longest 30%, i.e.
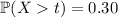
Transform to the standard normal distribution:
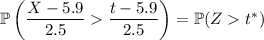
where
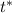
is the z-score corresponding to the cutoff time
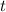
, which is approximately
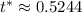
. Solve for
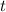
: