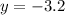Given the equation of a parabola:
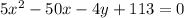
• You can rewrite it in Standard Form by following these steps:
1. Add the y-term to both sides of the equation:
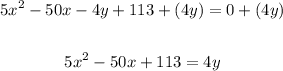
2. Subtract the Constant Term from both sides of the equation:
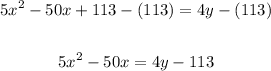
3. Divide both sides of the equation by 5 (the leading coefficient)
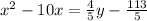
4. The coefficient of the x-term is:
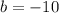
Then, you need to add this value to both sides:
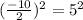
Therefore.
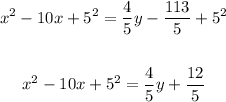
5. Rewrite the equation as follows:
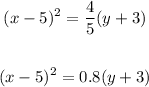
• Having the equation written in Standard Form:
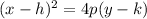
You can identify that:
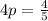
Solving for "p", you get:
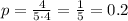
• You can identify that:
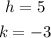
Therefore, the Vertex is:
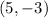
• By definition, the Focus of a parabola that opens upward is given by:
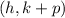
Then, in this case, this is:
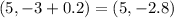
• By definition, the Directrix for a parabola that opens upward is given by:
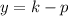
Then, in this case, you get:
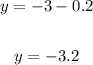
Hence, the answers are:
• Standard Form:

• Value for "p":
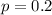
• Vertex:
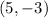
• Focus:
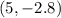
• Directrix: