Question

(1 point) The expression 64g4y2 64gʻy2 equals kg"ys where r, the exponent of g, is: and s, the exponent of y, is: and k, the leading coefficient is:

Answer 1

We are asked to find the final expression in exponent for, of the product of two radical expressions as shown below:

We will be addressing each factor at a time, first in the cubic root, and second in the square root.

Cubic root:

notice that the pure number (64) can be written as the perfect cube of the number 4 since 4^3 = 64. That means that a factor 4 will come out of the cubic root, and no factor 4 will be left in the root.

Now we are going to address the variables g and y which are inside the root, and try to find if they contain any perfect cube expression (perfect cubes will cancel out of the cubic root simplifying then the notation).

We notic that g^4 can be written as g^3 times g, so g^3 will come out of the cubic root as "g", and a factor "g" would be left inside the cubic root. Similarly, the factor y^2 cannot get out of the cubic root because it doesn't have a perfect cube in it.

We are then left with the following expression:

`4g\sqrt[3]{g\cdot y^2}`

Now, we recall the property of fractional exponents associated with roots of a factor:

`\sqrt[n]{x}=x^{(1)/(n)}`

Using this, the cubic root can be expressed as fractional exponents, as we show below:

`4g\sqrt[3]{g\cdot y^2}=4g\cdot g^{(1)/(3)}\cdot y^{(2)/(3)}=4g^{(4)/(3)}\cdot y^{(2)/(3)}`

Now we proceed to simplify the expression with the square root. This is much simpler, since all factor inside can be written as perfect squares:

64 = 8^2

g^4 = (g^2)^2 (the double square of g)

y^2 is already a perfect square.

Therefore, the square root is simplified entirely and we are left with the following factors:

8 g^2 y

Now we combine via the multiplication what we found for the cubic root and what we found for the square root:

`(4\cdot g^{(4)/(3)}\cdot y^{(2)/(3)})\cdot(8\cdot g^2\cdot y)=32\cdot g^{(10)/(3)}\cdot y^{(5)/(3)}`

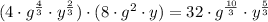
Therefore the power (r) of the factor g is the fraction: 10/3

The power (s) of the factor y is the fraction 5/3

and the constant number "k" is 32.