a) The Length of BC ≈ 99.72 cm
b) The area of Triangle ABC ≈ 1482.135 cm²
c) The size of the angle ABC ≈ 72.86°
a) Length of BC using Law of Cosines:
The Law of Cosines states that for any triangle ABC with sides a, b, and c, and angle C opposite side c:
c² = a² + b² - 2ab cos(C)
In this case, we have:
BC² = AB² + AC² - 2ABAC cos(BAC)
Substitute the given values:
BC² = 57² + 48² - 2 * 57 * 48 * cos(117°)
Calculate BC:
BC =

BC ≈
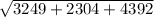
BC ≈
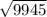
BC ≈ 99.72 cm
b) Area of Triangle ABC:
The area (A) of a triangle can be calculated using the formula:
A = 1/2 * base * height
AB as the base, the length of AB = 57 cm, and find the height.
We can use the sine of angle BAC to find the height:
height = AB * sin(BAC) = 57 * sin(117°)
The area:
Area = 1/2 * 57 * 57 * sin(117°)
Area ≈ 1/2 * 57 * 57 * 0.927
Area ≈ 1482.135 cm²
c) Angle ABC using Law of Sines:
The Law of Sines states that for any triangle ABC with sides a, b, and c, and opposite angles A, B, and C:
sin(A)/a = sin(B)/b = sin(C)/c
We already know angle BAC (117 degrees) and sides AB and BC. We can use this information to find angle ABC:
sin(ABC) =
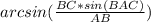
Now, find the angle ABC:
ABC =

ABC ≈ arcsin(1.221)
ABC ≈ 1.27 radians
ABC ≈ 72.86°