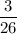Question

A juggler has a bag containing three yellow balls, six green balls, three blue balls, and one red ball, all the same size. The juggler pulls a ball from the bag at random. Then, without replacing it, he pulls out a second ball. What is the probability that the juggler first draws a green ball followed by a blue ball?

Answer 1

lets put in the mind first we are finding a probability for without replacement.

Here we have 6 green,3 blue,1red balls
Probability of picking a green ball=Total Green/Total
which is going to be P1 =6/6+3+1=6/10=0.6

Now we are not putting back green ball in the bag again
Probability of Blue ball=Total blue balls/Total(new)
P2 =3/9=0.33

Now total will become 1 less than before as we did not put green ball back in the bag.

Now add them up =p1+p2=0.6+0.33=0.27

Answer 2

Answer:
`(3)/(26)`

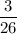
Explanation:

Given: The number of green balls in bag =6

Total number of balls =
`3+6+3+1=13`

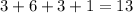
The probability of drawing first ball is green is given by :-

`P(G)=(6)/(13)`

Since he didin't replace first ball, then the total number of remains = 12

The number of blue balls in the bag = 3

The probability of drawing second ball is blue is given by :-

`P(B)=(3)/(12)`

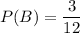
Now, the probability that the juggler first draws a green ball followed by a blue ball is given by :-

`P(G)* P(B)=(6)/(13)*(3)/(12)=(3)/(26)`

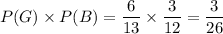
The probability that the juggler first draws a green ball followed by a blue ball :
`(3)/(26)`