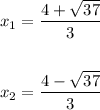Given the function:

Find the first derivative:
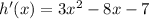
The first derivative gives us the slope of the tangent line to the graph of the function. When the tangent line is horizontal, the slope is 0, thus:

This is a quadratic equation with coefficients a = 3, b = -8, c = -7.
To calculate the solutions to the equation, we use the quadratic solver formula:
![$$x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}$$](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/fd0rgdksya0ov61axoi4.png)
Substituting:
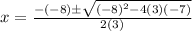
Operate:
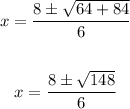
Since:

We have:
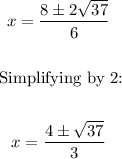
There are two solutions: