Question

Write out the first few terms of the Picard iteration scheme for each of the following initial value problems. Where possible, find explicit solutions and describe the domain of this solution.

a) x'=x+2 ; x(0)=2
b) x'=x^(4/3) ; x(0)=0
c) x'=x^(4/3) ; x(0)=1

Answer 1

Given an ODE
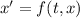
`x'=f(t,x)` with initial condition
`x(t_0)=x_0`, the general process is to write the ODE as an integral equation,


`x(t)=x_0+\displaystyle\int_(t_0)^tf(u,x(u))\,\mathrm du`

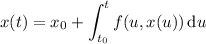
By setting
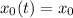
`x_0(t)=x_0` for all
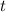
`t`, we get the following recurrence for
`n\ge1`.


`x_(n+1)(t)=x_0+\displaystyle\int_(t_0)^tf(u,x_n(u))\,\mathrm du`

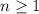
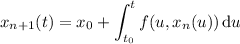
From this we work towards finding a pattern for
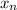
`x_n` so that we can find a solution of the form
`x=\lim\limits_(n\to\infty)x_n`.


`\begin{cases}x'=x+2\\x(0)=2\end{cases}`

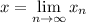
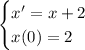
Write this as the integral equation,


`x_(n+1)=x(0)+\displaystyle\int_(t_0)^t(x_n(u)+2)\,\mathrm du`

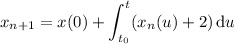
First step:


`x_1=x(0)+\displaystyle\int_(t_0)^t(x_0(u)+2)\,\mathrm du`

`x_1=2\displaystyle\int_0^t\mathrm du`

`x_1=2t`

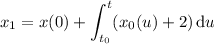
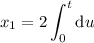
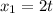
Second step:


`x_2=x(0)+\displaystyle\int_(t_0)^t(x_1(u)+2)\,\mathrm du`

`x_2=\displaystyle\int_0^t(2u+2)\,\mathrm du`

`x_2=t^2+2t`

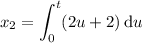
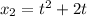
Third step:


`x_3=x(0)+\displaystyle\int_(t_0)^t(x_2(u)+2)\,\mathrm du`

`x_3=\displaystyle\int_0^t(t^2+2t+2)\,\mathrm du`

`x_3=\frac13t^3+t^2+2t`

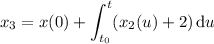
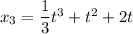
Fourth step:


`x_4=x(0)+\displaystyle\int_(t_0)^t(x_3(u)+2)\,\mathrm du`

`x_4=\displaystyle\int_0^t\left(\frac13u^3+u^2+2u+2\right)\,\mathrm du`

`x_4=\frac1{4*3}t^4+\frac13t^3+t^2+2t`

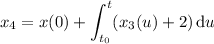
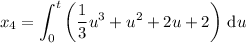
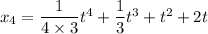
You should already start seeing a pattern. Recall that


`e^t=\displaystyle\sum_(k=0)^\infty(x^k)/(k!)=1+t+\frac{t^2}2+(t^3)/(2*3)+(t^4)/(2*3*4)+\cdots`

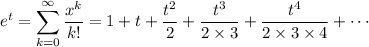
Multiplying this by 2 gives


`2e^t=2+2t+t^2+\frac{t^3}3+(t^4)/(4*3)+\cdots`

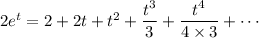
which matches the solution we have for
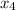
`x_4` except for that first term. So subtracting that, we find a solution of


`x=2e^t-2`

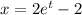
with a domain of
`t\in\mathbb R`.

Hopefully this gives some insight on how to approach the other two problems.