Question

A certain isotope decays so that the amount A remaining after t years is given by: A = A0 · e ^-0.03t where A0 is the original amount of the isotope. To the nearest year, the half-life of the isotope (the amount of time it takes to decay to half the original amount) is how many years?

Answer 1

Ending Amt = Bgng Amt * e ^-0.03t
In this equation, the "-0.03" is the decay factor or "k"
We can now solve for half-life by this equation:
t = (ln [y(t) ÷ a]) ÷ -k (we can say beginning amount = 200 and ending amount = 100
t = (ln [200 ÷ 100]) ÷ -k
t = (ln [2]) ÷ -k
t = 0.69314718056 ÷ --.03
t = 23.1049060187
about 23 years

Answer 2

The number of years is approximately 23 years.

Explanation:

Given : A certain isotope decays so that the amount A remaining after t years is given by :
`A = A_0\cdot e^(-0.03t)` where
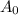`A_0` is the original amount of the isotope.

To find : To the nearest year, the half-life of the isotope (the amount of time it takes to decay to half the original amount) is how many years?

Solution :

The decay model is given by
`A = A_0\cdot e^(-0.03t)`

We have given that,

The amount of time it takes to decay to half the original amount.

i.e.
`A=(A_0)/(2)`

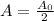
Substitute the values in the formula,

`A=A_0e^(-0.03t)`

`(A_0)/(2)=A_0e^(-(0.03)t)`

`(1)/(2)=e^(-(0.03)t)`

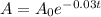
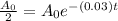
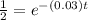
Taking natural log both side,

`\ln(1)/(2)=\ln e^(-(0.03)t)`

`-\ln2=-(0.03)t\ln e`

`t=(-\ln2)/(-0.03)`

`t=23.10`

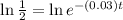
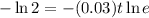
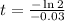
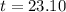
Therefore, The number of years is approximately 23 years.