Question

James Bond is unconscious in a 1000kg car full of explosive on a very dangerous road. After starting from rest at the top of the hill (point A), the car reaches the flat (horizontal) part of the road. At the beginning of the flat(horizontal) part, Bond regains the consciousness and applies brakes. The car skids across the horizontal road while slowing. The car, full of explosive, stops just as it reaches the far edge of the 50 m flat (horizontal) part of the road. What constant breaking force would have to be applied for the car to make a safe stop in a horizontal distance of 50 m?

Answer 1

F = 19600 N

Step-by-step explanation:

After reading this interesting exercise, I think you are missing the diagram, but we are going to solve them assuming the height of the hill, point A of about h = 100m.

Let's start by using the concepts of energy, to find the speed at the bottom of the hill

Starting point. Point A highest part of the colima

Em₀ = U = m g h

Final point. Flat part.

`Em_(f)` = k = ½ m v²

as they tell us that there is no friction, energy is conserved

Em₀ = Em_{f}

mgh = ½ m v²

v = √2gh

let's calculate

v = √ (2 9.8 100)

v = 44.27 m / s

Now we can use the scientific expressions, when it stops its speed is zero

v² = v₀² - 2 a x

0 = v₀² - 2ax

a =
`( v_(o)^2 )/(2x)`

a =
`( 44.27^(2) )/( 2 \ 50)`

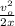
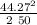
a = 19.6 m / s²

with this acceleration we use Newton's second law

f = m a

F = 1000 19.6

F = 19600 N