Question

What is the correlation coefficient with the following data points:

(1,6), (3,2), (7,5), (6,2)?

A.) 0.27
B.) -0.27
C.) 0.28
D.) -0.28

Answer 1

Option D → -0.28 Explanation:

Given : Data points : (1,6), (3,2), (7,5), (6,2)

To find : What is the correlation coefficient with the following data points?

Solution :

Let x= 1,3,7,6

And y=6,2,5,2

N is the number of points i.e, N=4

The formula of correlation coefficient is

`r=\frac{n(\sum xy)-(\sum x)(\sum y)}{\sqrt{{(n\sum x^(2)-(\sum x)^(2))(n\sum y^(2)-(\sum y)^(2))}}}`

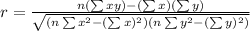
Now, we find term by term

`\sum x = 1+3+7+6=17`

`\sum y = 6+2+5+2=15`

`\sum xy = 6+6+35+12=59`

`\sum x^(2)= 1+9+49+36=95`

`\sum y^(2)=36+4+25+4=69`

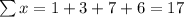
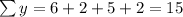
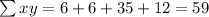
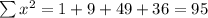
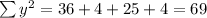
Substitute all the values in the formula,

`r=\frac{4(59)-(17)(15)}{\sqrt{{(4(95)-(17)^(2))(4(69)-(15)^(2))}}}`

`r=\frac{236-255}{\sqrt{{(380-289)(276-225)}}}`

`r=\frac{-19}{\sqrt{{(91)(51)}}}`

`r=(-19)/(√(4641))`

`r=(-19)/(68.12)`

`r=-0.278`

`r\approx -0.28`

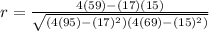
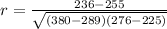
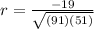
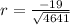
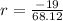
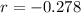
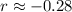
Therefore, The correlation coefficient is -0.28.

So, Option D is correct.