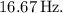Question

A 6.00-m long string sustains a three-loop standing wave pattern as shown. The wave speed is 2.00 × 102 m/s.What is the lowest possible frequency for standing waves on this string?

Answer 1

The lowest frequency for standing waves on a long string with a wave speed of
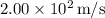`\(2.00 * 10^2 \, \text{m/s}\)` is approximately
`\(16.67 \, \text{Hz}\)`.

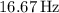To determine the lowest possible frequency for standing waves on the 6.00-meter long string, we can use the formula:

`\[ f = (v)/(2L) \]`

where:

-
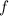`\( f \)` is the frequency,

-
`\( v \)` is the wave speed,

-
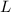`\( L \)` is the length of the string.

In this case, the wave speed
`(\( v \))` is given as
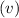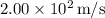`\(2.00 * 10^2 \, \text{m/s}\)`, and the length of the string
`(\( L \))` is 6.00-meters. Substituting these values into the formula:

`\[ f = \frac{2.00 * 10^2 \, \text{m/s}}{2 * 6.00 \, \text{m}} \]`

Simplifying the expression:

`\[ f = \frac{100 \, \text{Hz}}{6} \]`

`\[ f \approx 16.67 \, \text{Hz} \]`

Therefore, the lowest possible frequency for standing waves on the 6.00-meter long string is approximately
`\(16.67 \, \text{Hz}\).`

Answer 2

Given:

The length of the string is l = 6 m

The speed of the wave is

`v=2*10^2\text{ m/s}`

Required: Lowest possible frequency for the standing wave.

Step-by-step explanation:

The lowest possible frequency is the fundamental frequency.

The fundamental frequency can be calculated by the formula

`f=(v)/(2l)`

On substituting the values, the fundamental frequency will be

`\begin{gathered} f=(2*10^2)/(2*6) \\ =16.67\text{ Hz} \end{gathered}`

Final Answer: The lowest possible frequency for standing waves on this string is 16.67 Hz