Answer:
C.
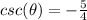
D.
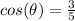
Explanation:
First, take a look to the picture I attached you. I drew a diagram according to the data provided from the problem. From this diagram:

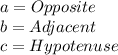
Now, the functions on a right triangle like this are given by:
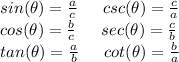
If:
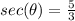
Then:
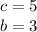
Using pythagorean theorem we can find a:
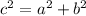
Solving for a:
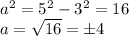
Since the triangle is in the fourth quadrant, the value of the opposite angle is negative, hence:
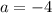
Now, let's check every option, so we can determinate which of them are true or false.
A.
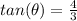
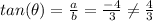
This is incorrect.
B.
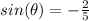
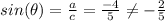
This is incorrect.
C.
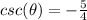
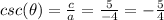
This is correct
D.
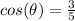
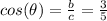
This is correct.