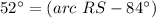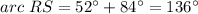Question

If arc SQ = 84° and ∠RPS = 26°, what is the measure of arc RS?

Answer 1

`arc\ RS=136\°`

Explanation:

see the attached figure to better understand the problem

we know that

The measurement of the external angle is the semi-difference of the arcs which comprises

In this problem

m∠RPS=
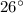`26\°` ------> external angle

so

m∠RPS=
`(1)/(2)(arc\ RS-arc\ SQ)`

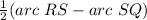
we have

m∠RPS=
`26\°`

`arc\ SQ=84\°`

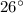
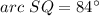
substitute the values

`26\°=(1)/(2)(arc\ RS-84\°)`

Solve for arc RS

`52\°=(arc\ RS-84\°)`

`arc\ RS=52\°+84\°=136\°`

Answer 2

if we assume that S is as tangent point, we can have the following formula:
(arcRS - arcSQ)/2 = ∠RPS= (arc RS - 84°) /2=26°
it means arc RS - 84° = 52°, and then meas arc RS = 52+84=136°