Question

Sketch the graph of the polynomial function. Use synthetic division and the remainder theorem to find the zeros.

Answer 1

GIVEN:

We are given the following polynomial;

`f(x)=x^4-2x^3-25x^2+2x+24`

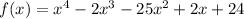
Required;

We are required to sketch the graph of the function. Also, to use the synthetic division and the remainder theorem to find the zeros.

Step-by-step solution;

We shall begin by sketching a graph of the polynomial function.

From the graph of this polynomial, we can see that there are four points where the graph crosses the x-axis. These are the zeros of the function. One of the zeros is at the point;

`(-1,0)`

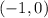
That is, where x = -1, and y = 0.

We shall take this factor and divide the polynomial by this factor.

The step by step procedure is shown below;

Now we have the coefficients of the quotient as follows;

`1,-3,-22,24`

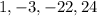
That means the quotient is;

`x^3-3x^2-22x+24`

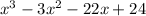
We can also divide this by (x - 1) and we'll have;

We now have the coefficients of the quotient after dividing a second time and these are;

`x^2-2x-24`

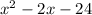
The remaining two factors are the factors of the quadratic expression we just arrived at.

We can factorize this and we'll have;

`\begin{gathered} x^2-2x-24 \\ \\ x^2+4x-6x-24 \\ \\ (x^2+4x)-(6x+24) \\ \\ x(x+4)-6(x+4) \\ \\ (x-6)(x+4) \end{gathered}`

The zeros of this polynomial therefore are;

`\begin{gathered} f(x)=x^4-2x^3-25x^2+2x+24 \\ \\ f(x)=(x+1)(x-1)(x-6)(x+4) \\ \\ Where\text{ }f(x)=0: \\ \\ (x+1)(x-1)(x-6)(x+4)=0 \end{gathered}`

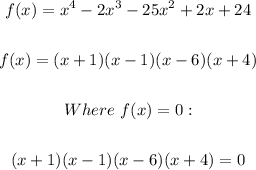
Therefore;

ANSWER:

`\begin{gathered} x+1=0,\text{ }x=-1 \\ \\ x-1=0,\text{ }x=1 \\ \\ x-6=0,\text{ }x=6 \\ \\ x+4=0,\text{ }x=-4 \end{gathered}`