Answer:
Half life of the radioactive element is 5 days.
Explanation:
Formula to get the final amount after the radioactive decay in 't' days,
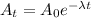
Here
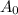 = Initial amount
= Initial amount
λ = Decay constant
t = duration of decay
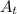 = Final amount
= Final amount
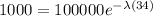
0.01 =
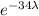
ln(0.01) =

-4.6052 = -34λ
λ = 0.13544
Since, λ =
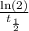
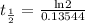
= 5.11
≈ 5 days
Therefore, half life of the radioactive element is 5 days.