Question

How many of the numbers from 10 through 92 have the sum of their digits equal to a perfect​ square?

Answer 1

All the numbers in this range can be written as
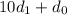
`10d_1+d_0` with
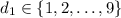
`d_1\in\{1,2,\ldots,9\}` and
`d_2\in\{0,1,\ldots,9\}`. Construct a table like so (see attached; apparently the environment for constructing tables isn't supported on this site...)

so that each entry in the table corresponds to the sum of the tens digit (row) and the ones digit (column). Now, you want to find the numbers whose digits add to perfect squares, which occurs when the sum of the digits is either of 1, 4, 9, or 16. You'll notice that this happens along some diagonals.

For each number that occupies an entire diagonal in the table, it's easy to see that that number
`n` shows up
`n` times in the table, so there is one instance of 1, four of 4, and nine of 9. Meanwhile, 16 shows up only twice due to the constraints of the table.

So there are 16 instances of two digit numbers between 10 and 92 whose digits add to perfect squares.