Question

An insurance company offers flood insurance to customers in a certain area. Suppose they charge $500 fora given plan. Based on historical data, there is a 1% probability that a customer with this plan suffers aflood, and in those cases, the average payout from the insurance company to the customer was $10,000.Here is a table that summarizes the possible outcomes from the company's perspective:EventFloodPayout Net gain (X)$10,000 -$9,500$0$500No floodLet X represent the company's net gain from one of these plans.Calculate the expected net gain E(X).E(X) =dollars

Answer 1

The given is a discrete random variable.

For a discrete random variable, the expected value is calculated by summing the product of the value of the random variable and its associated probability, taken over all of the values of the random variable.

It is given that the probability of a flood is 1%=0.01.

It follows that the probability of no flood is (100-1)%=99%.

Hence, the expected net gain is:

`E(X)=0.01(-9500)+0.99(500)=-95+495=400`

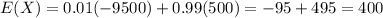
Hence, the expected net gain is $400.

The expected net gain is E(X) = $400.