Question

Given a soda can with a volume of 36 and a diameter of 4, what is the volume of a cone that fits perfectly inside the soda can? (Hint: only enter numerals in the answer blank). (4 points)

Answer 1

First we need to find the heigh of the soda can be rearanging the volume formula, . We can make that We know that V is 36 and radius is half of the diameter, so radius is 2.

h = 2.87

Now, we can use the height to figure out the volume of a cone. The volume of a cone is
R is 2 again and h is 2.87


12.56*.96 = 12.0576
So a cone with a volume of 12.0576 is the largest that will fit into the soda can

Answer 2

12 unit³

Explanation:

Soda can is in the form of a cylinder.

So volume of a soda can =
`\pi r^(2) h`

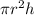
where volume of can = 36 unit³

and r =
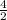`(4)/(2)` units = 2 unit

Now from the given formula

36 = (2)² (h) π

36 = 4 h × π

h =
`(36)/(4)=(9)/(\pi )`

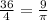
Now we have to calculate the volume of a cone that fits perfectly inside the can.

Volume of cone
`=(1)/(3)(\pi r^(2)h)`

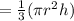
Height of cone = height of can =
`(9)/(\pi )` unit

Radius of cone = radius of can = 2 unit

volume of cone =
`(1)/(3)(\pi )(2)^(2)` ×
`((9)/(\pi ) )`

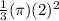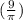
= 3 × 4

= 12 unit³