A construction worker drops a hammer from a height of 25 m. How long will it take the hammer to hit the ground? Use the formula  h(t)=-4.9t^2+v_o+h_o , where v_o is the initial…

Question

A construction worker drops a hammer from a height of 25 m.

How long will it take the hammer to hit the ground?
Use the formula 
`h(t)=-4.9t^2+v_o+h_o` , where
`v_o` is the initial velocity and
`h_o` is the initial height.
Round to the nearest tenth of a second. Enter your answer in the box.
___s

Answer 1

Answer: 2.3 seconds

Explanation:

Given: A construction worker drops a hammer from a height of
`h_(o)=25\ meter`.

Using formula
`h(t)=-4.9t^2+v_(o)+h_(o)` , where
`v_o` is the initial velocity and
`h_o` is the initial height.

Put t=0, the initial velocity = 0m/s in the beginning.

`h(t)=-4.9t^2+0+25=4.9t^2+25`

When the hammer hits the ground, then height
`h_(o)=0\ meter`

`h(t)=-4.9t^2+25\\\\\Rightarrow 0=-4.9t^2+25\\\\\Rightarrow 4.9t^2=25\\\\\Rightarrow t^2=5.\\\\\Rightarrow\ t=√(5.1)=\pm2.2583179581\approx \pm2.3`

`\\\\\Rightarrow t=2.3\ seconds` [Since time is a positive quantity.]

Answer 2

Time at which the hammer reaches the ground is 2.3 seconds.

Explanation:

We are given the formula as,
`h(t)=-4.9t^2+v_(o)+h_(o)`.

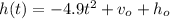It is known that, when height i.e.
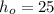`h_(o)=25` meter, then velocity
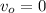`v_(o)=0` m/sec.

So, we get the formula as,
`h(t)=-4.9t^2+25`.

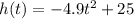Now, when the hammer hits the ground, the height
`h_(o)=0` meter.

Thus, we have,

`h(t)=-4.9t^2+25`

⇒
`0=-4.9t^2+25`

⇒
`4.9t^2=25`

⇒
`t^2=5.1`

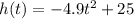
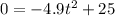
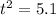
i.e. t= ±2.3 sec

Since, time cannot be negative.

So, t= 2.3 sec

Hence, the time at which the hammer reaches the ground is 2.3 seconds.