Answer:
-288
Explanation:
Geometric Sequence is the sequence in which every digit is the same multiplier of its previous digit.
The formula of Geometric Sequence is:

Here we have given that, a₁ = -8, r = 6
So, for finding the 3rd term, n = 3
∵

∴
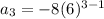
⇒ a₃ = -8 × 36 = -288
Thus, third term is -288.