Question

∠ACE is formed by two secants intersecting outside of a circle. If minor arc BD = 28°, minor arc AB = 112°, and minor arc DE = 112°, what is the measure of ∠ACE?

Answer 1

Angle ACE = 40 degrees

Answer 2

∠ACE = 40°

Explanation:

Refer the attached figure .

Since we know that sum of measures of all arcs is 360°

arc AE + arc AB +arc BD +arc DE = 360°

arc AE+ 252°=360°

arc AE=360°

-252°

arc AE=108°

Now to find the ∠ACE , we will use the theorem.

Theorem : If two secants intersect to form the vertex of an angle outside a circle and the sides of the angle intercept arcs on the circle,then the measure of the angle is equal to one-half the difference of the measures of the arcs intercepted by the sides of the angle.

For∠ACE

The arcs intercepted by the sides of the angle.: arc AE =108° and arc BD=28°

So, by theorem :

`\angle ACE = (1)/(2)(\text{arc AE - arc BD})`

`\angle ACE = (1)/(2)* (108^(\circ) - 28^(\circ))`

`\angle ACE = (1)/(2)* 80^(\circ)`

`\angle ACE = 40^(\circ)`

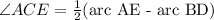
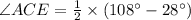
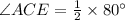
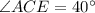
Hence the measure of ∠ACE is 40°