Question

Assume that f is continuous on [-4,4] and differentiable on (-4,4). The table gives some values of f'(x) x: -4, -3, -2, -1, 0, 1, 2, 3, 4 f'(x): 74, 39, 10, -6, -14, -12, 0, 22, 55 a) estimate where f is increasing, decreasing, and has local extrema.

Answer 1

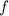
`f` will be increasing on the intervals where
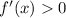
`f'(x)>0` and decreasing wherever
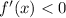
`f'(x)<0`. Local extrema occur when
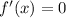
`f'(x)=0` and the sign of
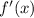
`f'(x)` changes to either side of that point.


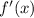
`f'(x)` is positive when
`x` is between -4 and some number between -2 and -1, and also 2 (exclusive) and 4, so you can estimate that
`f(x)` is increasing on the intervals [-4, -2] and (2, 4].


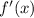
`f'(x)` is negative when
`x` is between some number between -2 and -1, up to some number less than 2. So
`f(x)` is decreasing on the interval [-1, 1].

You then have two possible cases for extrema occurring. The sign of
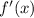
`f'(x)` changes for some
`x` between -2 and -1, and again to either side of
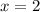
`x=2`.