Question

What is the maximum height of h(t)=-16t^2+16t+480

Answer 1

There's a negative in a, so it would have an invisible -1 multiplying the whole equation.

`-1(16t^2-16t-480)`
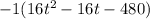
Then you take two numbers that multiply to 16*-480
and add to -16. Let's hide out the -1 for now until the end to make it easier for us.
In this case, it would be -96 and 80 because 16*-480 = -7680 and multiplying -96 by 80 results in same product while adding up to -16.
Then you put those numbers in.

`(16t^2-96t+80t-480)`
Start to factor them by adding brackets and using GCF to separate them.

`(16t^2-96t)+(80t-480)`
Again, with GCF to simplify even more.

`16t(t-6)+80(t-6)`
And re-arrange to form the numbers into factored form cause of distributive property.

`(16t+80)(t-6)`
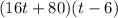
GCF to simplify to lowest terms.

`16(t+5)(t-6)`
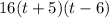
Bring back the -1 we hid.

`-16(t+5)(t-6)`
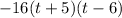Important Note: in vertex and factored form, the plus/positive signs within the brackets mean left side into negative x-values, and negative signs within brackets mean right side into positive x-values. In this case, your x-intercepts/zeros are (-5,0) and (6,0).

A person can't go into negative time, so they start from 0 and hit into the positive number of the x-int, so that's (6,0). 6 seconds. Find midpoint by adding the two x-int and dividing by 2.

`h= (-5+6)/(2) \\ \\ h= (1)/(2)`
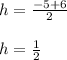
Take the midpoint and plug into your quadratic equation to find your max height. Use a calculator for this.