Question

Graph the function and state the domain and range.g(x)=x^2-2x-15Domain-Range-Graphed function-

Answer 1

Answer:

The domain: -∞ < x < ∞

The range: g(x) ≥ -16

Step-by-step explanation:

The given function is:

`g(x)\text{ = x}^2\text{-2x-15}`

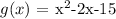
The domain is a set of all the valid inputs that can make the function real

All real values of x will make the function g(x) to be valid

The domain: -∞ < x < ∞

The range is the set of all valid outputs

From the function g(x):

a = 1, b = -2

`\begin{gathered} (b)/(2a)=(-2)/(2(1))=-1 \\ g(-1)=(-1)^2-2(-1)-15 \\ g(-1)=1-2-15 \\ g(-1)=-16 \end{gathered}`

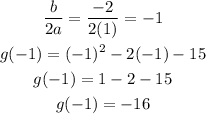
Since a is positive, the graph will open upwards

Therefore, the range of the function g(x) is: g(x) ≥ -16

The graph of the function g(x) = x^2 - 2x - 15 is plotted below