Question

Which of the following describes the zeroes of the graph of f(x) = 3x6 + 30x5 + 75x4?

–5 with multiplicity 2 and 1/3 with multiplicity 4
5 with multiplicity 2 and 1/3 with multiplicity 4
–5 with multiplicity 2 and 0 with multiplicity 4
5 with multiplicity 2 and 0 with multiplicity 4

Answer 1

The answer is (c) -5 with a multiplicity 2 and 0 with multiplicity 4

Answer 2

option C : –5 with multiplicity 2 and 0 with multiplicity 4

Explanation:

`f(x) = 3x^6 + 30x^5 + 75x^4`

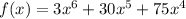
To find out zeros of the graph we need to factor the given polynomial

Also replace f(x) with 0

`0 = 3x^6 + 30x^5 + 75x^4`

`0= 3x^4(x^2 + 10x +25)`

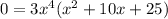
Factor x^2 +10x+25, product =25 and sum is 10

5*5=25, 5+5=10

`0= 3x^4(x+5)(x+5)`

`0= 3x^4(x+5)^2`

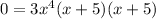
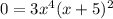
3x^4 =0, so x=0 with multiplicity 4

(x+5)^2 =0 , x=-5 with multiplicity 2