Question

In the school election James ran against Ben for secretary James received 75% of the votes if 240 students voted how many votes did James not receive?

Answer 1

Answer: James did not received 60 votes.

Explanation:

Given: In a school election,

Percentage of votes received by James = 75%

Percentage of voted hadn't received by James = 100% - 75% = 25%

If 240 students voted , the number of votes hadn't received by James= 25% of 240

`=(25)/(100)* 240\\\\=\frac14*240\\\\=60`

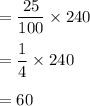
Hence, James did not received 60 votes.