Answer:
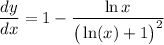
General Formulas and Concepts:
Calculus
Differentiation
- Derivatives
- Derivative Notation
Derivative Property [Addition/Subtraction]:
![\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]](https://img.qammunity.org/2018/formulas/mathematics/high-school/44u8gzhn9ta01w8xtfd21jo1ablmtfakai.png)
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Product Rule]:
![\displaystyle (d)/(dx) [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)](https://img.qammunity.org/2018/formulas/mathematics/college/fmesql9w8fux2f3pm7q5e1vbby82cqcoak.png)
Derivative Rule [Quotient Rule]:
![\displaystyle (d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))](https://img.qammunity.org/2018/formulas/mathematics/college/ooo3i8krh214thjb98380rs5e4a9gzlyyc.png)
Explanation:
Step 1: Define
Identify
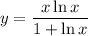
Step 2: Differentiate
- Derivative Rule [Quotient Rule]:
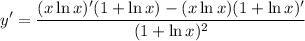
- Derivative Rule [Product Rule]:
 - (x \ln x)(1 + \ln x)')/((1 + \ln x)^2)](https://img.qammunity.org/2018/formulas/mathematics/college/8q9kmdy95my3dyuxv0uwmricml0dgw4sgq.png)
- Logarithmic Differentiation [Derivative Properties]:
 - \ln x)/((1 + \ln x)^2)](https://img.qammunity.org/2018/formulas/mathematics/college/2s0hox1w4jvqxdewq4mbusf6179kwlzbm1.png)
- Basic Power Rule:
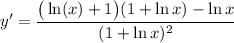
- Simplify:
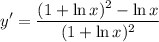
- Rewrite:
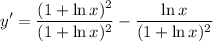
- Simplify:
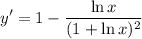
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Differentiation