Question

Kite WXYZ is graphed on a coordinate plane. What is the approximate perimeter of the kite? Round to the nearest tenth. 10.6 units 11.5 units 14.0 units 16.2 units

Answer 1

D. 16.2 units.

Explanation:

We have been given an image of a kite on coordinate plane and we are asked to find the perimeter of our given kite.

Since we know that a kite has two disjoint pairs of congruent consecutive sides, so the perimeter of our given kite will be 2 times the sum of side XY and YZ.

To find the length of sides XY and YZ we will use distance formula.

`\text{Distance}=√((x_2-x_1)^2+(y_2-y_1)^2)`

Upon substituting coordinates of point X and Y in above formula we will get,

`\text{Distance between point X and Y}=√((3-5)^2+(4-1)^2)`

`\text{Distance between point X and Y}=√((-2)^2+(3)^2)`

`\text{Distance between point X and Y}=√(4+9)`

`\text{Distance between point X and Y}=√(13)`

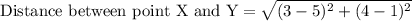
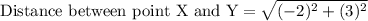
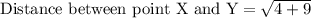
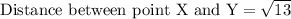
Now similarly we will find the length of segment YZ.

`\text{Distance between point Y and Z}=√((5-3)^2+(1--3)^2)`

`\text{Distance between point Y and Z}=√((2)^2+(1+3)^2)`

`\text{Distance between point Y and Z}=√(4+(4)^2)`

`\text{Distance between point Y and Z}=√(4+16)`

`\text{Distance between point Y and Z}=√(20)`

`\text{Distance between point Y and Z}=2√(5)`

`\text{Perimeter of kite WXYZ}=2(XY+YZ)`

`\text{Perimeter of kite WXYZ}=2(√(13)+2√(5))`

`\text{Perimeter of kite WXYZ}=2(3.6055512754639893+4.4721359549995794)`

`\text{Perimeter of kite WXYZ}=2(8.0776872304635687)`

`\text{Perimeter of kite WXYZ}=16.1553744609271374\approx 16.2`

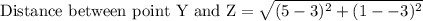
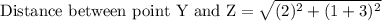
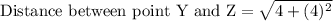
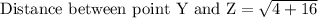
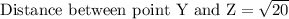
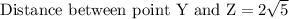
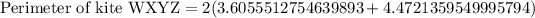
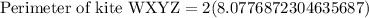
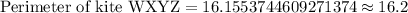
Therefore, the perimeter of the kite WXYZ is 16.2 units and option D is the correct choice.

Answer 2

Perimeter of the kite is 16.2 units

Solution-

As WXYZ is a kite, so two disjoint pairs of consecutive sides are congruent, i.e WX=XY and WZ=ZY

So, perimeter of the kite WXYZ is,

`=2(\overline{WX}+\overline{WZ})`

And

`\overline{WX}=√((1-3)^2+(1-4)^2)=√((-2)^2+(-3)^2)=√(4+9)=√(13)`

`\overline{WZ}=√((1-3)^2+(1+3)^2)=√((-2)^2+(4)^2)=√(4+16)=√(20)`

So, perimeter will be,

`P=2(√(13)+√(20))=16.15\approx 16.2\ units`