Question

Which expression can be used to find the nth term in this sequence position: 1 2 3 4 5 nvalue of term: 2 5 10 17 26 ?

Answer 1

n²+1 where n is the position of the sequence

1) Considering the sequence (2,5,10,17,26,...) corresponding to 1,2,3,4,5,...

Let's figure out how that sequence grows:

5 -2 = 3

10 -5 = 5

17-10= 7

26-17= 9

And examining the differences from each difference we have:

5-3 =2

7-5 = 2

9-7 =2

2) So we can write the following table, where the first line is the sequence, then the positions, then the subtraction between them.

As it is a quadratic formula, we can write in the general form and then plug x=0

`\begin{gathered} a_n=n^2 \\ 2\text{ 5 10 17 26} \\ 1\text{ 2 3 4 5 6 } \\ 1\text{ 4 9 25 36} \\ a_n=n^2+0n+1 \\ a_n=n^2+1 \end{gathered}`

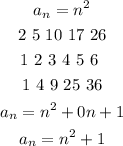
3) Hence, to find the 6th term, for instance, we plug n=6 so

6²+1 = 31. So the formula to find the nth term is n² +1

3) Finally, the sequence is given by n² +1 where n is the position of the term.